Groups and VGroups

Sometimes it is very necessary to group several Mobjects to apply some Manim method to them.

For example, suppose we want to apply a shift to several Mobjects, it is true that we can group them in an array and make a loop, but it is much faster to group them in a Group and apply the shift to that Group.

The difference between Group and VGroup is simple, Group supports any Mobject, such as ImageMobject and VMobjects, but VGroup only supports VMobjects.

Groups

Group support any method of Mobjects, such as shift, scale, move_to, next_to, align_to, etc. However you cannot apply VMobjects methods to them, such as set_stroke or set_fill, if you want to use those methods then you will have to use a VGroup.

Two additional methods that are very useful are arrange and arrange_in_grid, they work quite simply:

It should be noted that when we apply arrange or arrange_in_grid, all Mobjects move to the center of the screen.

VGroups

They are exactly the same as Groups, but you can apply the VMobjects methods, such as set_stroke, set_fill, set_style, etc.

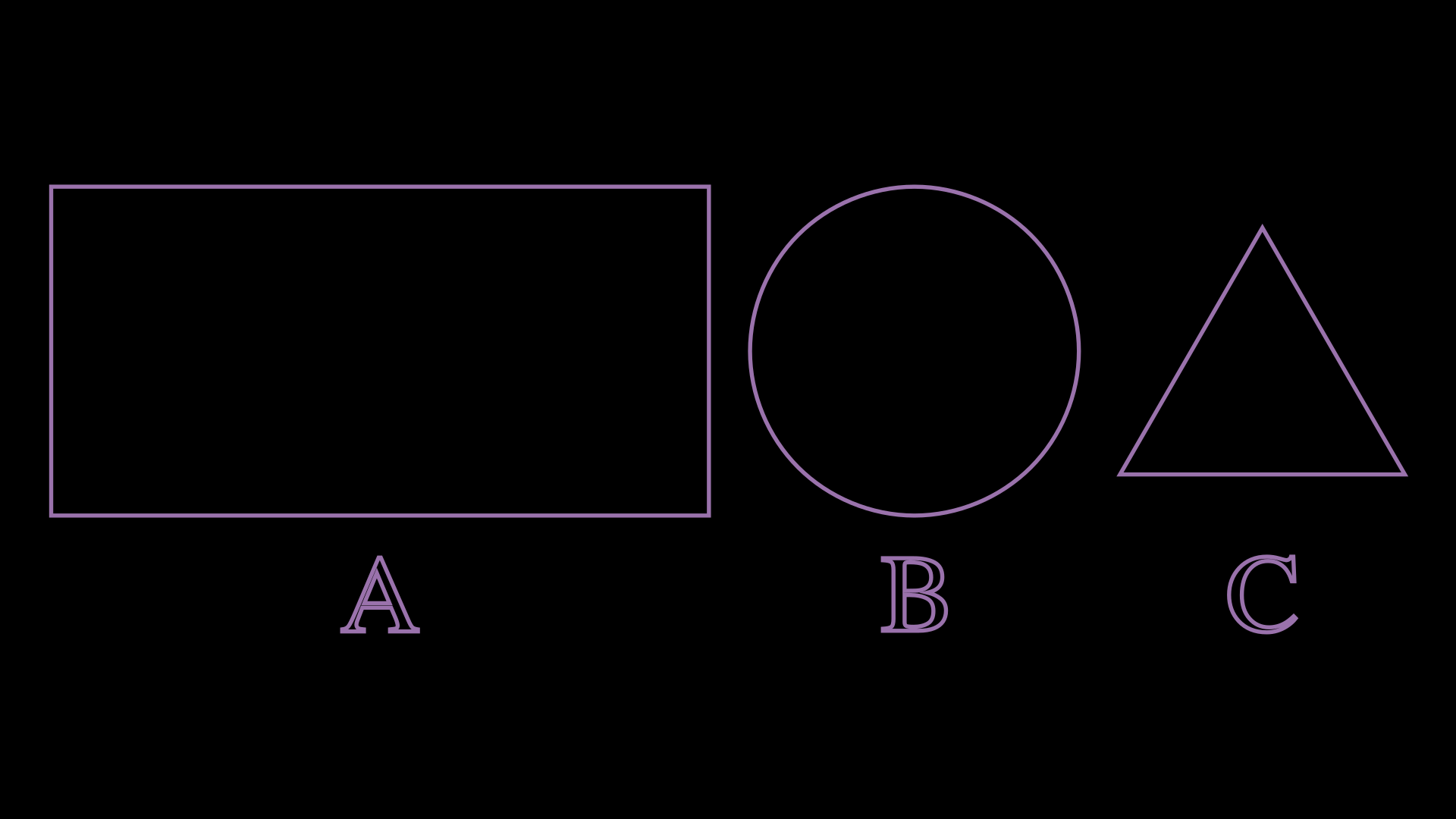
def construct(self):
    grp = VGroup(
        Rectangle(), Circle(), Triangle(),
        Text("A"),Text("B"),Text("C"),
    )
    grp.set_style(
        fill_opacity=0,
        stroke_width=4,
        stroke_color=PURPLE
    )
    grp.arrange_in_grid(cols=3)
    grp.width = config.frame_width - 1
    self.add(grp)

As arrays

Another advantage is that you can add, select and remove elements as you would with an array.

To add elements use Group.add(some_mobject)
To remove elements, use Group.remove(some_mobject), with the indication that some_mobject must already be included in the Group.
To select an item use Group[i] where i is a number, or a range, like Group[3:5]. If you use range then the return is another Group with those elements.

Using list comprehension

This technique is quite useful when we need to create Groups more quickly.

def construct(self):
    from itertools import cycle
    colors = cycle([RED,TEAL,ORANGE,PINK])
    grp = VGroup(*[
        Text(n,color=next(colors))
            .scale(4)
        for n in "ManimCE"
    ])
    grp.arrange(RIGHT,aligned_edge=DOWN)

    self.add(grp)

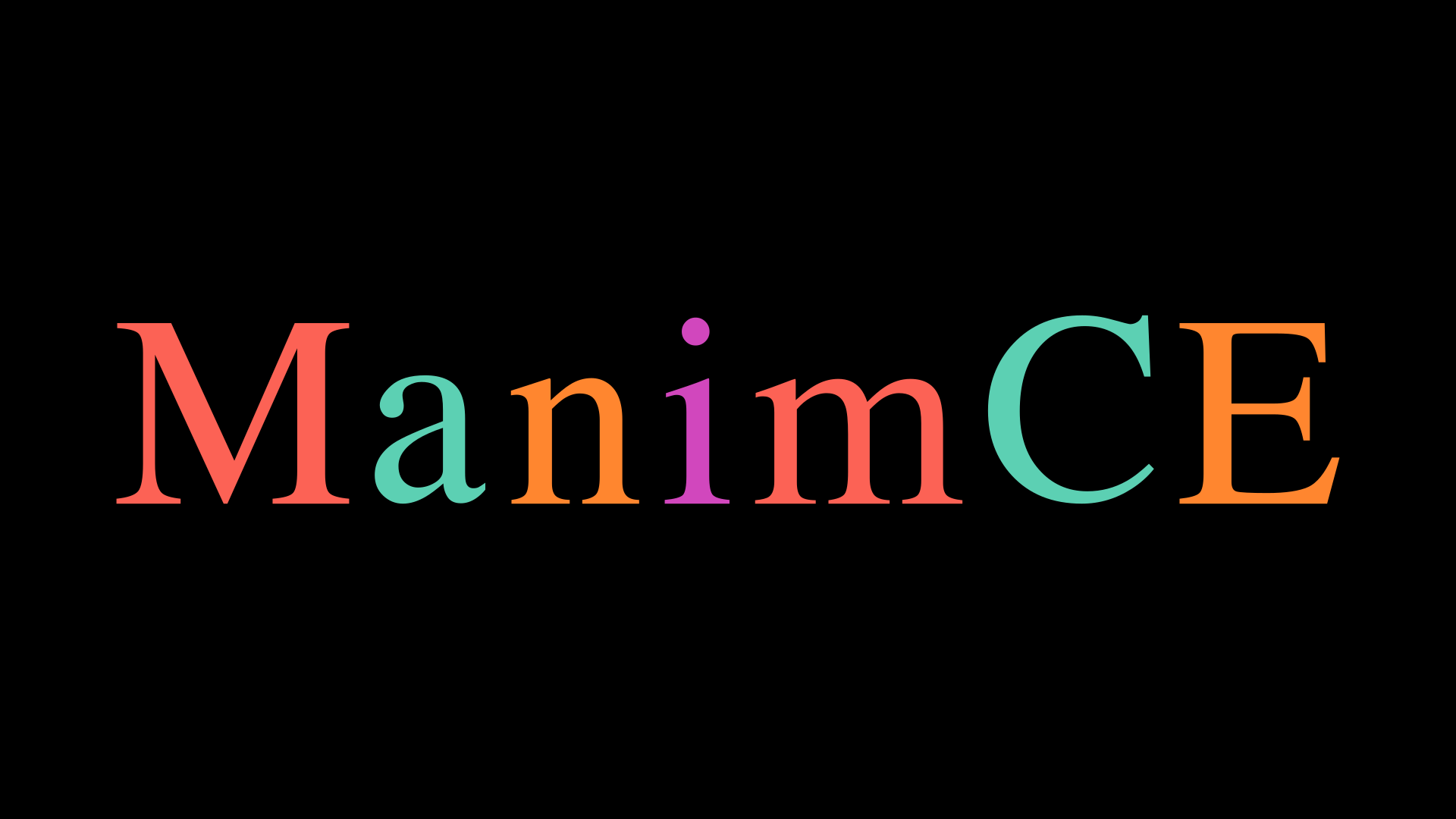
List comprehensions are quite useful in Manim, we will use them later in other chapters.